Arbitrary high-order, conservative and positivity preserving Patankar-type deferred correction schemes

This is a work in collaboration with Philipp Öffner.

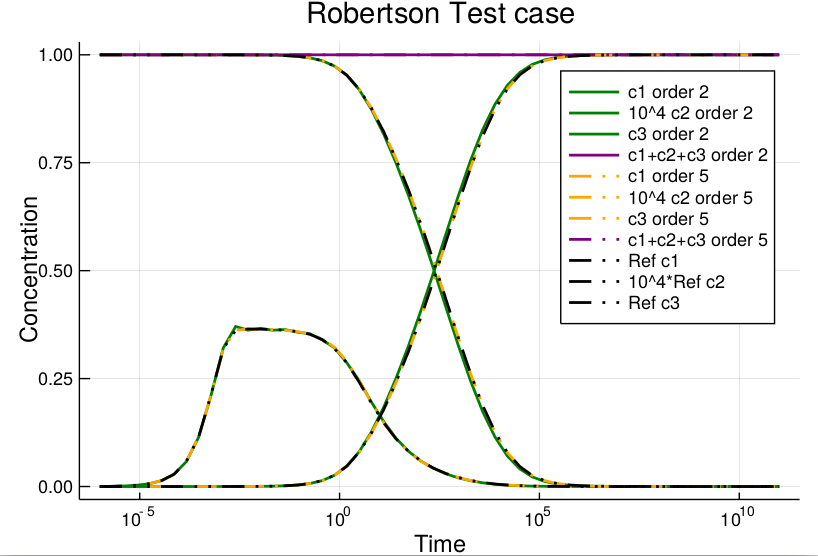
Production-destruction systems (PDS) of ordinary differential equations (ODEs) are used to describe physical and biological reactions in nature. The considered quantities are subject to natural laws. Therefore, they preserve positivity and conservation of mass at the analytical level. In order to maintain these properties at the discrete level, the so-called modified Patankar-Runge-Kutta (MPRK) schemes are often used in this context. However, up to our knowledge, the family of MPRK has been only developed up to third order of accuracy. In this work, we propose a method to solve PDS problems, but using the Deferred Correction (DeC) process as a time integration method. Applying the modified Patankar approach to the DeC scheme results in provable conservative and positivity preserving methods. Furthermore, we demonstrate that these modified Patankar DeC schemes can be constructed up to arbitrarily high order. Finally, we validate our theoretical analysis through numerical simulations.

Download paper
Journal page
arXiv page
BibTeX
You can find the code at this Git repository