Davide Torlo’s Personal Website
Hello visitor! I am Davide Torlo, an Assistant Professor (RTT, tenure track) at Università di Roma La Sapienza at Mathematics Department Guido Castelnuovo.
Previous positions:
- Postdoctoral Fellow at SISSA in prof. Rozza’s group
- Researcher at INRIA Bordeaux in CARDAMOM team, under the supervision of prof. Mario Ricchiuto
Education:
- PhD student at University of Zurich under the supervision of prof. Rémi Abgrall
- M.Sc. in SISSA and University of Trieste, thesis with prof. Gianluigi Rozza
- B.Sc. at University of Milan - Bicocca
Current research
My research interest is mainly focused on numerical methods for hyperbolic PDEs. In particular I study methods that are structure preserving and arbitrarily high order. I also study Model Order Reduction techniques for advection dominated problems and Fluid Structure Interaction problems.
Structure preserving methods
Many physical models are described by equations whose solutions verify certain properties. These physical properties are often of paramount importance and numerical methods should be able to preserve such properties. In the last years, I have developed several methods able of preserving different properties:
- positivity of the solution for example with modified Patankar (mP) schemes, starting from mPDeC schemes, studies on their Issues and with applications for Shallow Water equations
- entropy preserving/diffusing schemes, to find the physically relevant solution, see the relaxation DeC and relaxation ADER-DG approaches
- well-balancing some particular solutions as lake at rest states for shallow water in MPDeC for SW, global flux Finite Volume and Finite Element methods for shallow water and similar models, schemes to preserve the soliton behavior for dispersive waves equations or the divergence-free character.
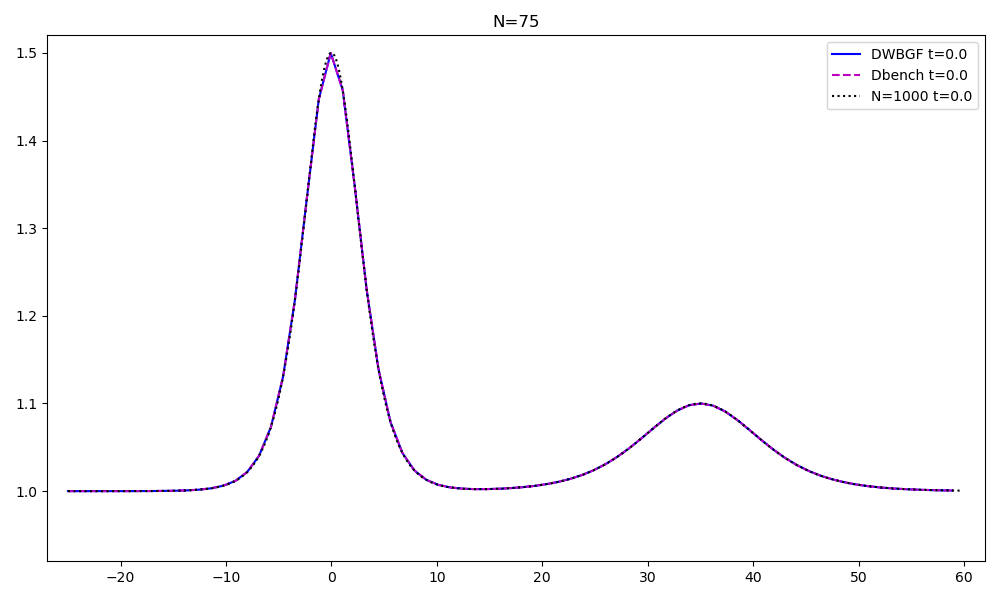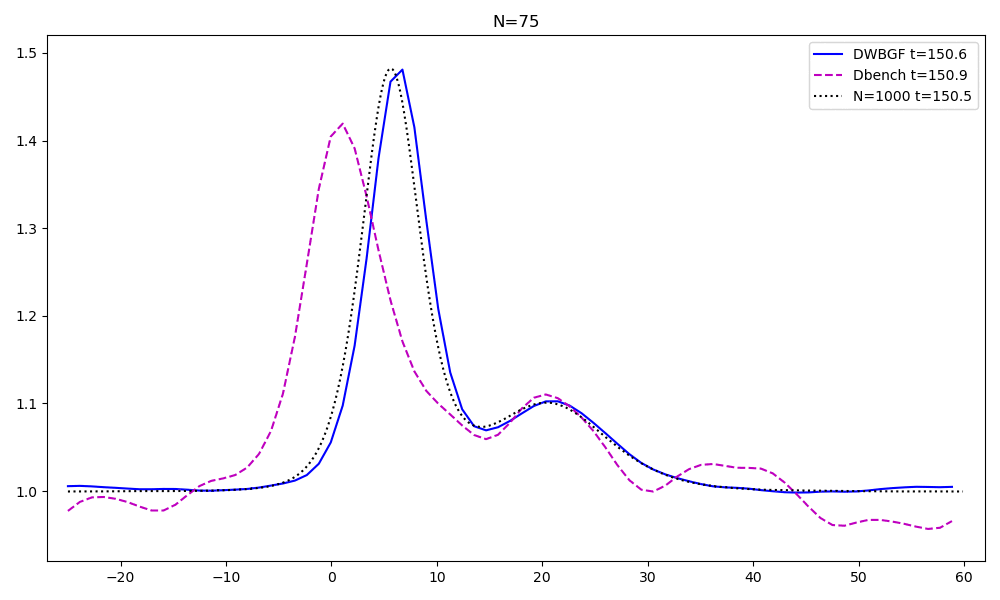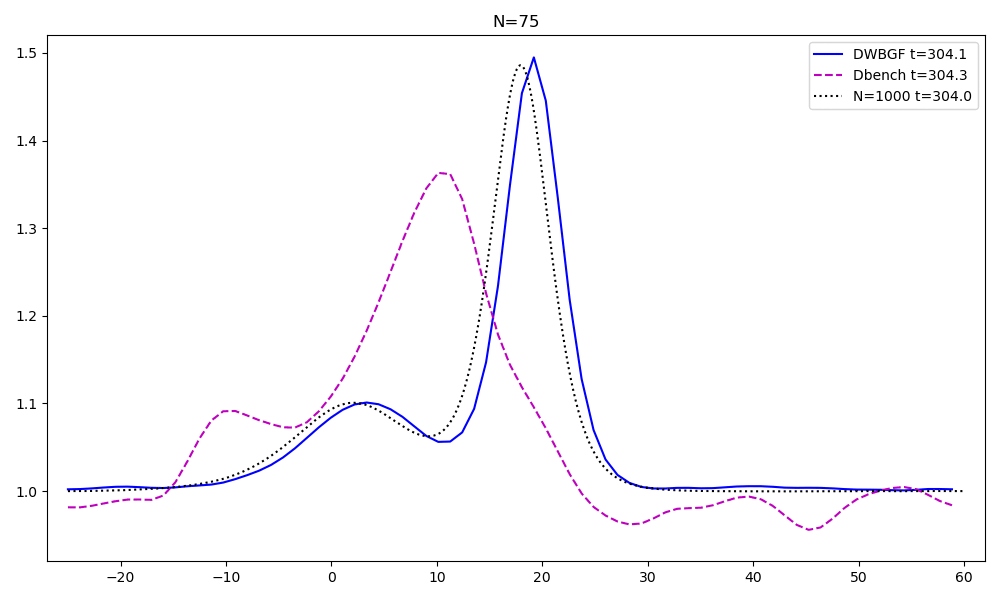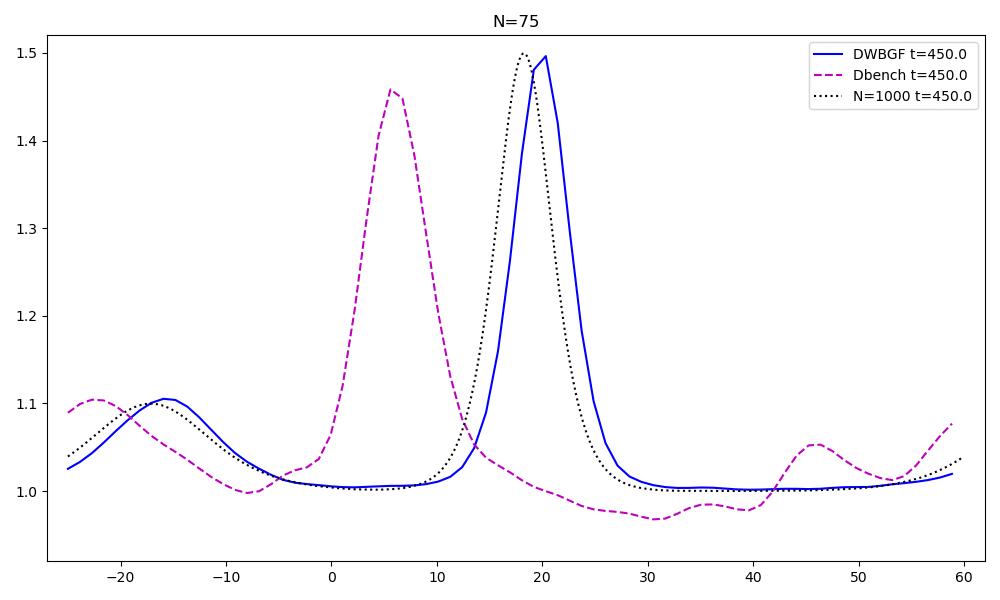
Reduced order models for advection dominated problems
These problems have a very slow decay of the Kolmogorov n-width. Hence, specific techniques must be used to obatain computational reduction. Ingredients that I retain fundamental in this topic are:
- an arbitrary-Lagrangian-Eulerian formulation, a geometrical calibration of the solutions, an optimization technique and a forecast of such calibration, see the preprint, now working on extending the process on multiple shocks and speeds
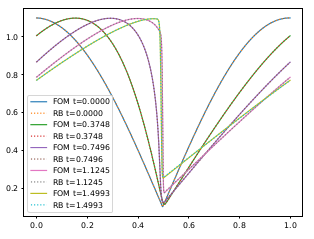
- nonlinear strategies including neural networks to tackle the problem, we are studying it now for Friedrichs’ Systems (talk) with Graph Neural Network to tackle the slow Kolmogorov n-width decay
Other more classical ROM have been used for dispersive wave equations, in UQ context, for advection-dominated problems or for domain decomposition.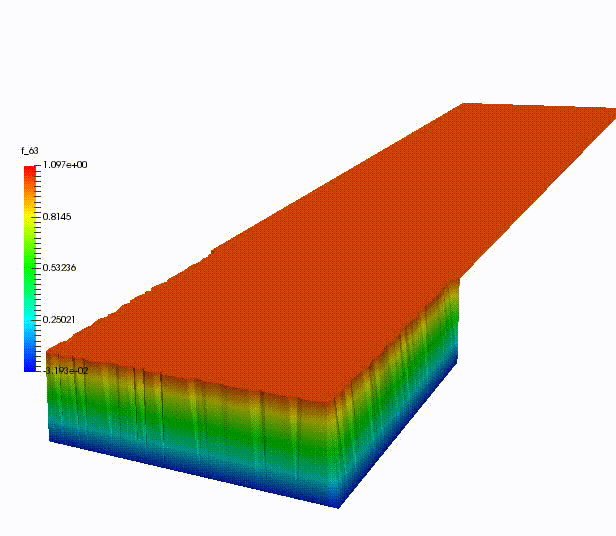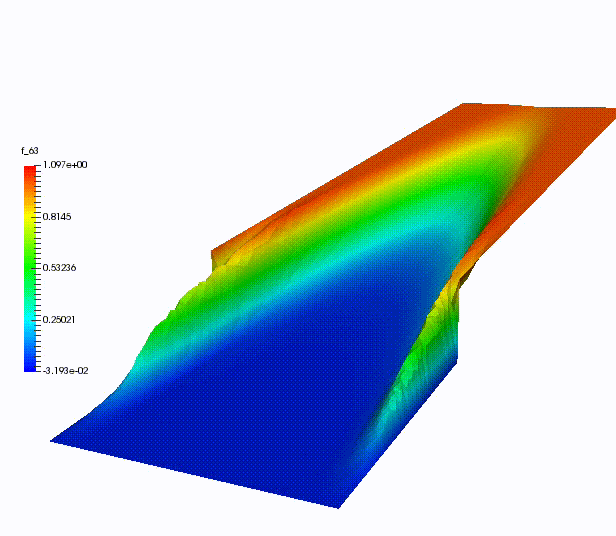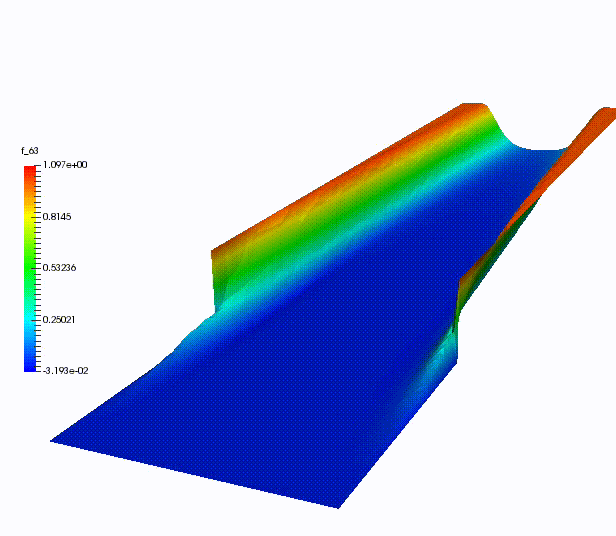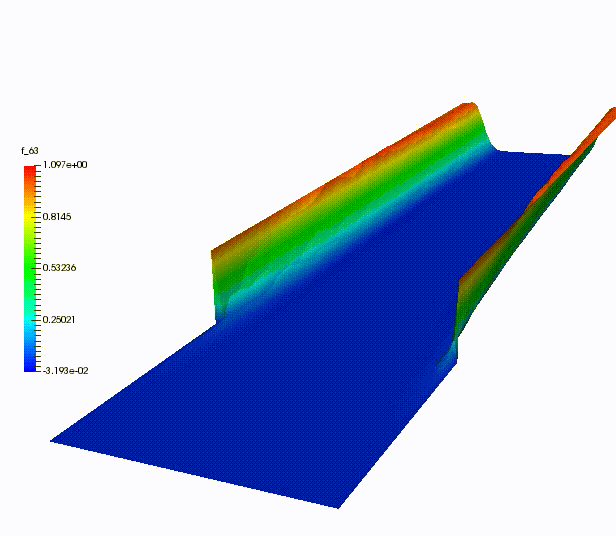 
Arbitrarily high order methods
Arbitrarily high order methods allow to obtain very accurate solutions within minimal computational costs. In particular, I have studied arbitrarily high order time integrations as Deferred Correction (DeC) and ADER and various spatial discretizations (finite element, finite volume, finite difference, spectral difference, discontinuous Galerkin).
- In the work ADER is DeC we compared the two methods as time discretization techniques.
- In the works efficient DeC and ADER DOOM we studied how to make these methods more efficient, p-adaptive and structure preserving methods.
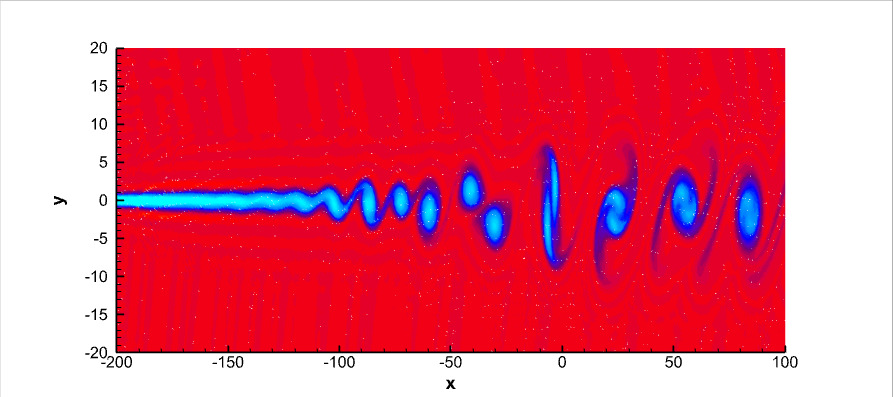
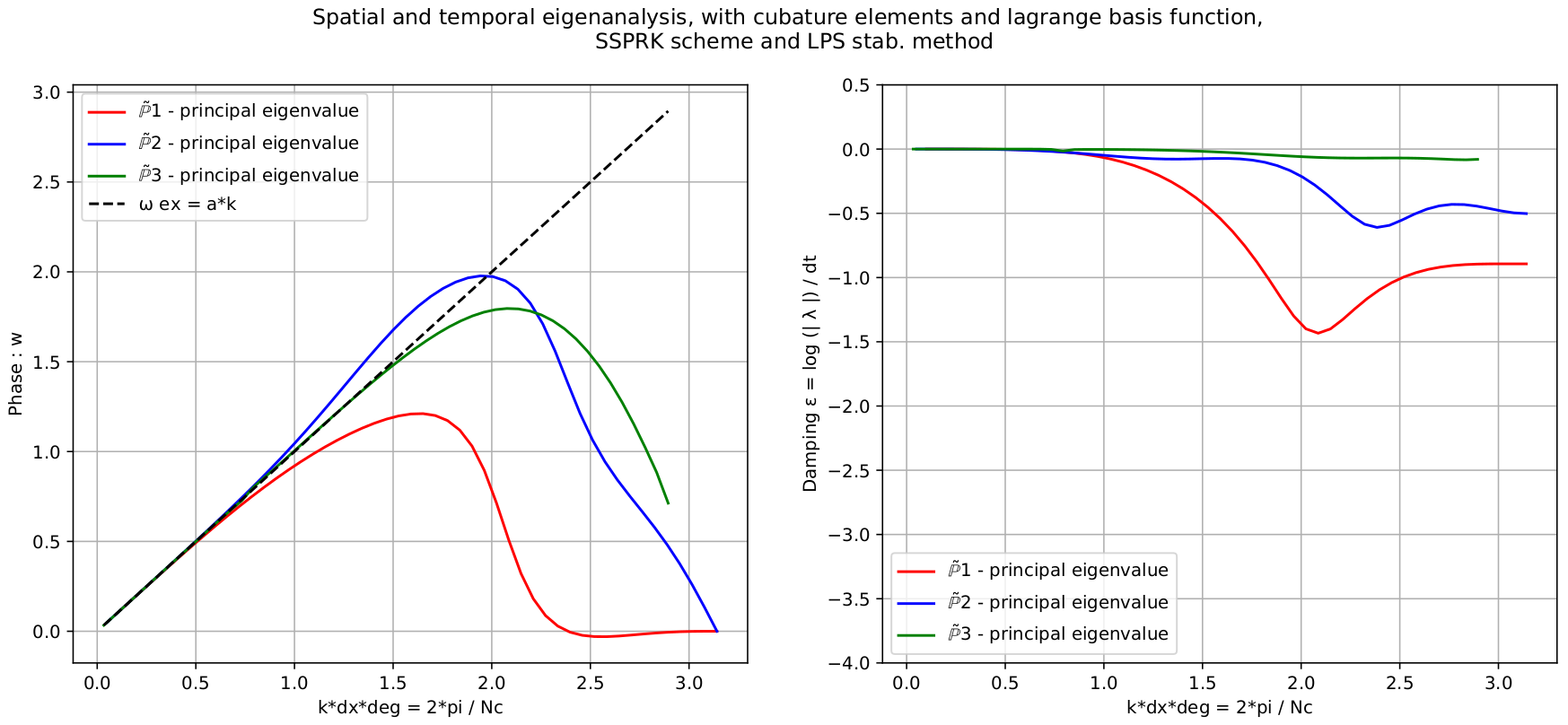
- For stabilized Finite Element methods in one dimension and in two dimensions on triangular meshes we are studying highly accurate space and time discretization for hyperbolic problems. We use different time integrators, space discretizations and stabilization techniques. The goal is to find the stability regions and the best perfomant scheme.
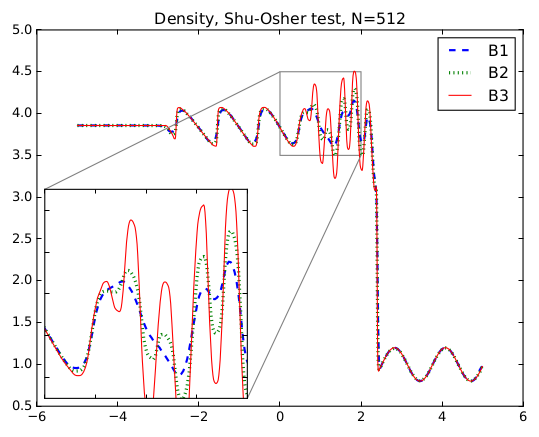
- Implicit–explicit discretization for kinetic models with arbitrary high order accuracy, through the Deferred Correction as time integration scheme and Residual distribution for the spatial discretization. IMEX DeC on residual distribution schemes and IMEX DeC on finite difference schemes
