High Order Asymptotic Preserving Deferred Correction Implicit-Explicit Schemes for Kinetic Models

This is a work in collaboration with Rémi Abgrall.

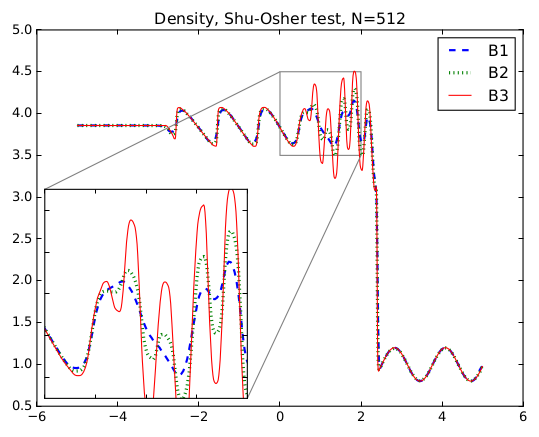
This work introduces an extension of the residual distribution (RD) framework to stiff relaxation problems. The RD is a class of schemes which is used to solve a hyperbolic system of partial differential equations. To our knowledge, it has been used only for systems with mild source terms, such as gravitation problems or shallow water equations. What we propose is an implicit-explicit (IMEX) version of the RD schemes that can resolve stiff source terms, without refining the discretization up to the stiffness scale. This can be particularly useful in various models, where the stiffness is given by topological or physical quantities, e.g., multiphase flows, kinetic models, or viscoelasticity problems. We will focus on kinetic models that are BGK approximation of hyperbolic conservation laws. The extension to more complicated problems will be carried out in future works. The provided scheme is able to catch different relaxation scales automatically, without losing accuracy; we prove that the scheme is asymptotic preserving and this guarantees that, in the relaxation limit, we recast the expected macroscopic behavior. To get a high order accuracy, we use an IMEX time discretization combined with a deferred correction procedure, while naturally RD provides high order space discretization. Finally, we show some numerical tests in one and two dimensions for stiff systems of equations.

Download paper
Journal page
arXiv page
BibTeX