Relaxation Deferred Correction Methods and their Applications to Residual Distribution Schemes

This is a work in collaboration with Rémi Abgrall, Elise Le Mélédo and Philipp Öffner.

In many models described by ordinary differential equations (ODEs) and partial differential equations (PDEs), there exists a scalar quantity that is physically conserved, e.g. energy, entropy, Liyapunov functional or angular momentum. Approximating with numerical methods the solutions of such models does not mean to automatically conserve these quantities. D. Ketcheson in Relaxation Runge-Kutta Methods: Conservation and stability for inner-product norms proposes a relaxation approach where each time step is relaxed by a factor $\gamma$. This means that the step that one actually does is a little more or a little less than the originally planned step. Properly tuning this $\gamma$, by solving a scalar (nonlinear) equation, one can guarantee to exactly conserve the desired quantity.

Without relaxation	With Relaxation

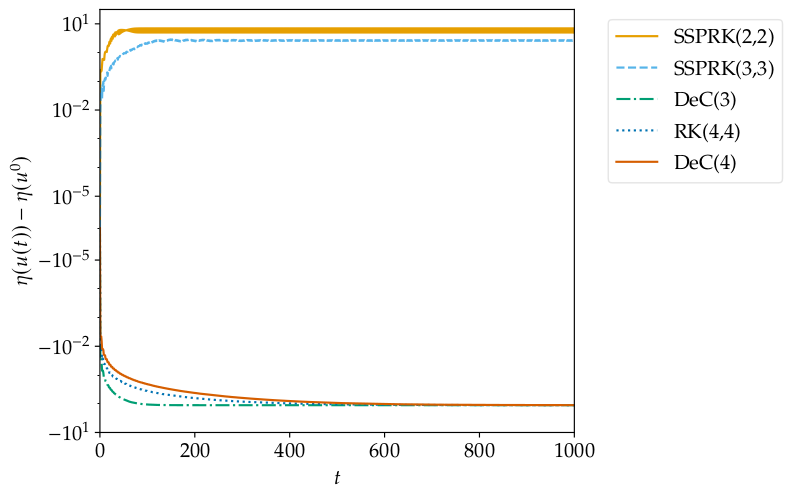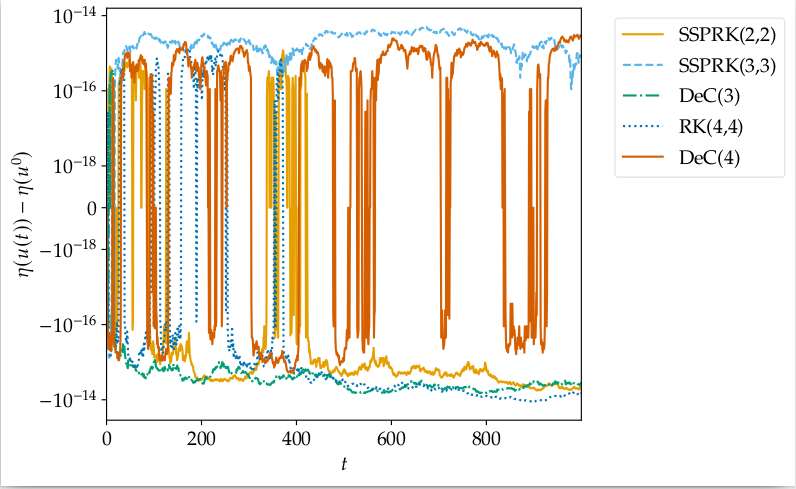In this work, we extend the relaxation algorithm to the class of arbitrarily high order accurate schemes defined by the Deferred Correction methods, Dutt Minion Abgrall. These methods can be used as method of lines, and hence, rewritten into Runge–Kutta methods, but they can also be used as iteration methods to converge to complicated high order discretizations using matrix free schemes. In that context, the relaxation technique can be applied in different ways.

Convergence of Relaxed DeC	Phase space evolution for a pendulum

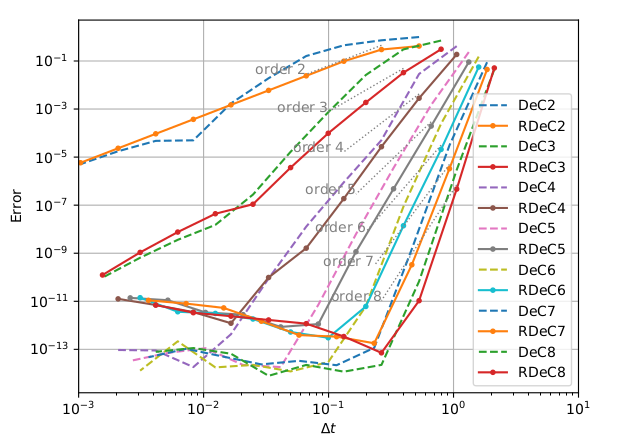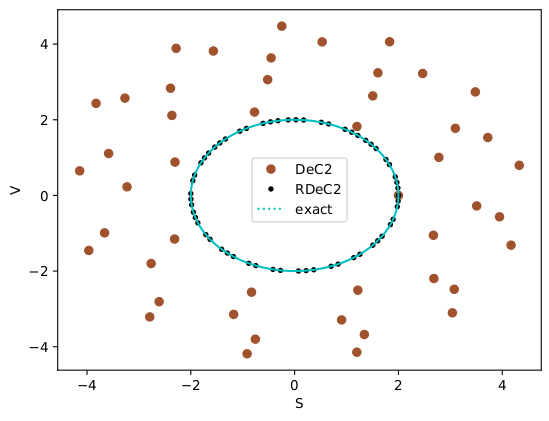Moreover, the whole procedure is limited by the necessity of having an entropy conservative/dissipative formulation of the spatial discretization, which fulfills the physical behavior of the solutions. We use the Entropy Fix approach by Abgrall, in the context of residual distribution to obtain either entropy conservative or entropy dissipative schemes.

Download paper
Journal page
arXiv page
BibTeX
You can find the code at this Git repository