Issues with Positivity-Preserving Patankar-type Schemes

This is a work in collaboration with Philipp Öffner and Hendrik Ranocha.

(Modified) Patankar-type schemes are linearly implicit time integration methods designed to be unconditionally positivity-preserving by going outside of the class of general linear methods for production–destruction systems (PDS). In practice, at every time stage a matrix is assembled using the production and destruction terms at the previous stages and a linear system must be solved. Thus, classical stability concepts cannot be applied and there is no satisfying stability theory for these schemes.

In particular, two issues appear. The first one is an oscillation issue around the steady state, which appear also for linear problems. These oscillations are common to all the schemes and can be observed only for large values of the timestep. In this work we find some CFL-type restrictions on the timesteps for all the schemes that seem to provide stability also for nonlinear cases.

CFL=1	CFL=2

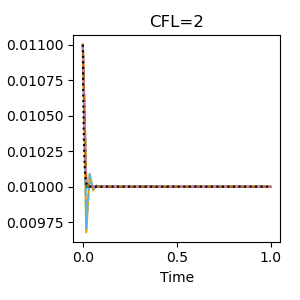The other issue that these methods show is loss of accuracy in the limit for initial conditions going to zero. This happens only for few of these scheme or for some specific parameters. We study analytically which of these schemes lose order of accuracy and we find the reduced order of accuracy for all presented schemes.

Download paper
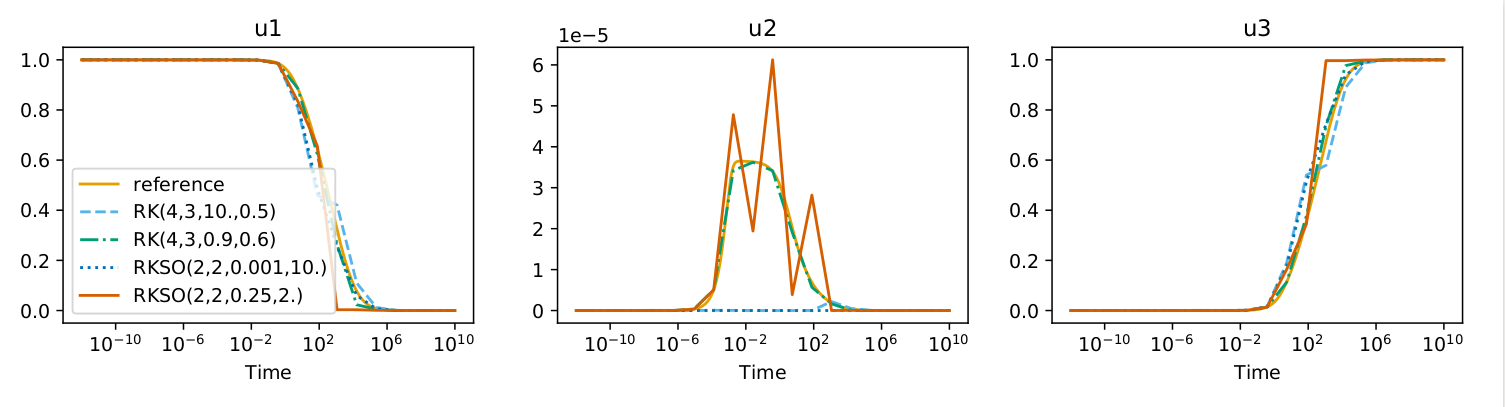
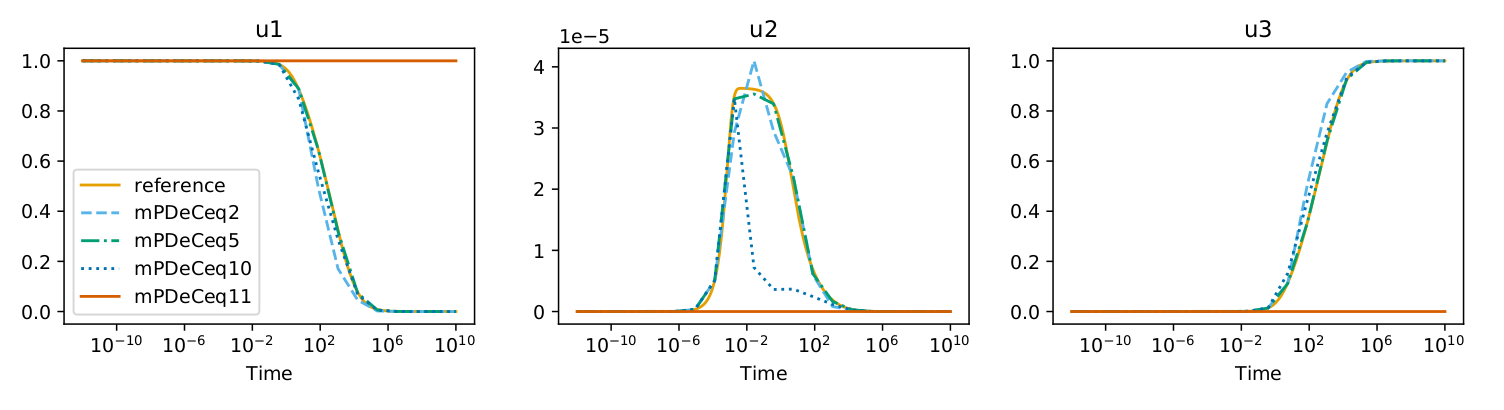
Journal page
arXiv page
BibTeX
You can find the code at this Git repository