Efficient iterative arbitrary high order methods: an adaptive bridge between low and high order

This work is in collaboration with Lorenzo Micalizzi and Walter Boscheri

Following the idea of the work on efficient DeC, we apply the same strategy for a more general framework. The idea is to take an arbitrarily high order iterative method, which increases the order of accuracy of the solution by one at each iteration, and match the discretization space at each iteration with the accuracy that will be reached at that iteration. The passage between different iterations can be performed in different ways and it consists in an embedding between two spaces one contained in the other. In this iterations, p-adaptivity can be performed by stopping the iterations when certain criteria are met. This is done through an a posteriori limiter: Discrete Optimally increasing Order Method (DOOM). Conversly to other a posteriori limiters, like MOOD, DOOM is completely local and waste-free. It can be performed along the iterations and as soon as it stops it already provides a reliable solutions without the need of recomputing any other method.

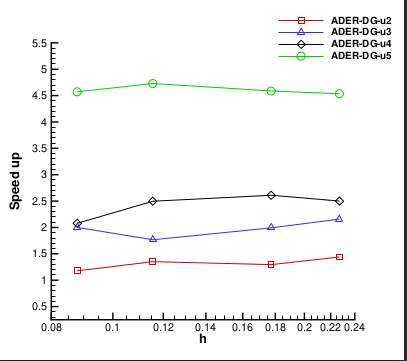
We apply this approach to ADER-DG and ADER-FV discretizations, obtaining provably positivity preserving schemes that we apply to Euler and Navier–Stokes equations. Below you see some simulations and the speed up that the method show with respect to the original formulation.

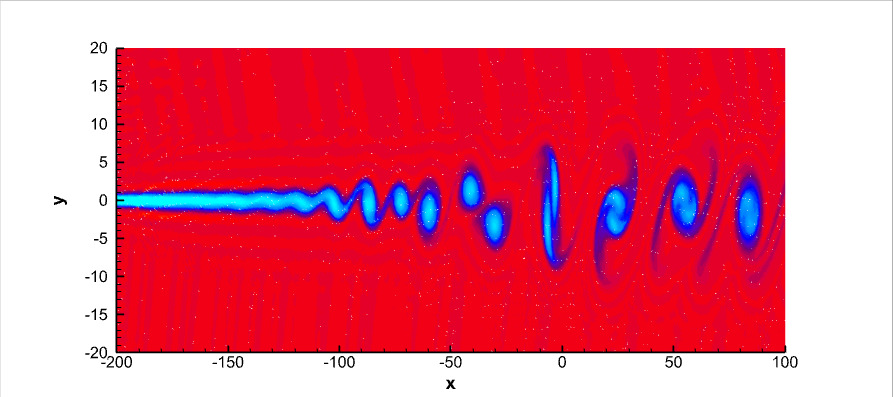
Speed Up	Two shocks

Download paper
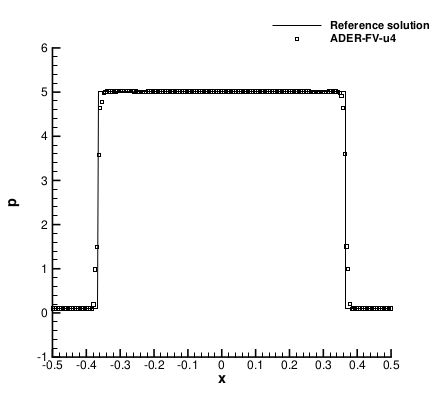Journal page
arXiv page
BibTeX