Weighted Model Order Reduction to Quantify Uncertainties

This is a blog post I wrote for the SISSA mathLab medium page.

Weighted Model Order Reduction to Quantify Uncertainties

Model order reduction (MOR) techniques, maybe familiar to many readers of this blog, are able to reduce computational time for numerical analysis (and not only) parametric problems. In a fast online phase of the MOR we exploit the expensive computations provided by an offline phase. This is useful in many situations, where fast evaluations of the map parameter-to-solution is necessary. We can think of real-time applications, where data are collected on the field and a fast response is necessary, optimization processes, where a cost function (depending on our parametric problem) must be evaluated several times, or uncertainty quantification (UQ) applications, where the parameters are intrinsically aleatory and the solution of the problem carries this uncertainty.

UQ is a broad subject and in this article we focus only parameter uncertainty and its possible stochastic behavior, i.e., we suppose that the parameters of our problem are random, but they obey to a known underlying probability law. The goal of this UQ task is to estimate what is the probability law of the solution of the problem, making use of the knowledge of the distribution of the parameters. Let us give an example. Suppose we have a parameter that follows a Beta(1.5,2) distribution. In the next figure on the left, we simulate the distribution of 10,000 samples drawn by this probability law. The goal of our UQ task is to understand the probability distribution for the output of the problem of interest, in the example below (right figure), a very simple function of the original parameter. What we observe in the figure is just a discrete approximation of the probability law.

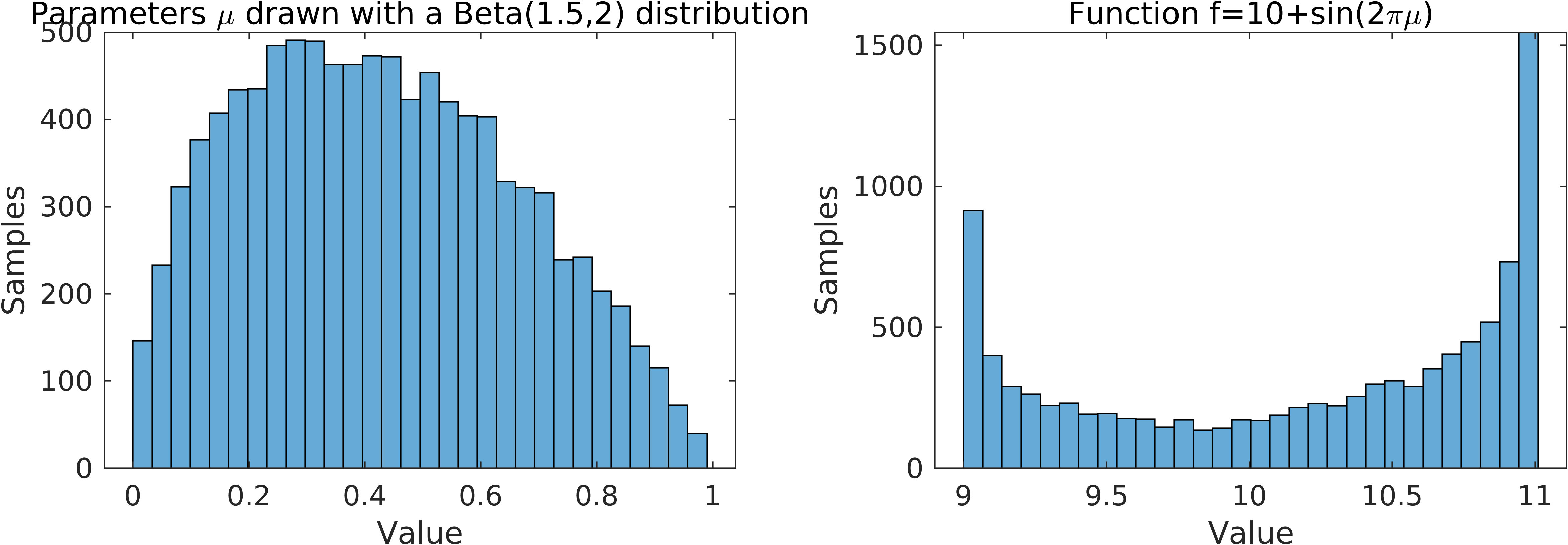
If one wants to get more insights on the law, it is important to compute some statistical momenta of the output solution, e.g. the mean and the variance of the solution, computed with sampling algorithms as Monte Carlo methods. Monte Carlo methods consists of computing the output problem for many parameters drawn from the probability law, as done in the previous picture, and then taking averages of the obtained quantities. The main issue of Monte Carlo methods is the slow decay of the error, which depends on the square root of the samples. In other words, if we want to have a tenth of the error we need to run 100 times the number of the original simulations. Hence, a very large number of samples are needed.

Here is where MOR helps the process.

Weighted model order reduction techniques

Let us summarise the main aspects of MOR algorithms. First of all, we have at our disposal a full order model (FOM), which provides reliable solutions in long computational times. MOR algorithms select some of these FOM solutions that constitute the reduced space where we search the reduced solution. One way to build a reduced model (ROM) is projecting on the reduced space the operators and use the reduced operators to find new reduced solutions. The ROM are often much smaller and faster to be solved, allowing to use way less computational time (up to 100, 1000 times faster).

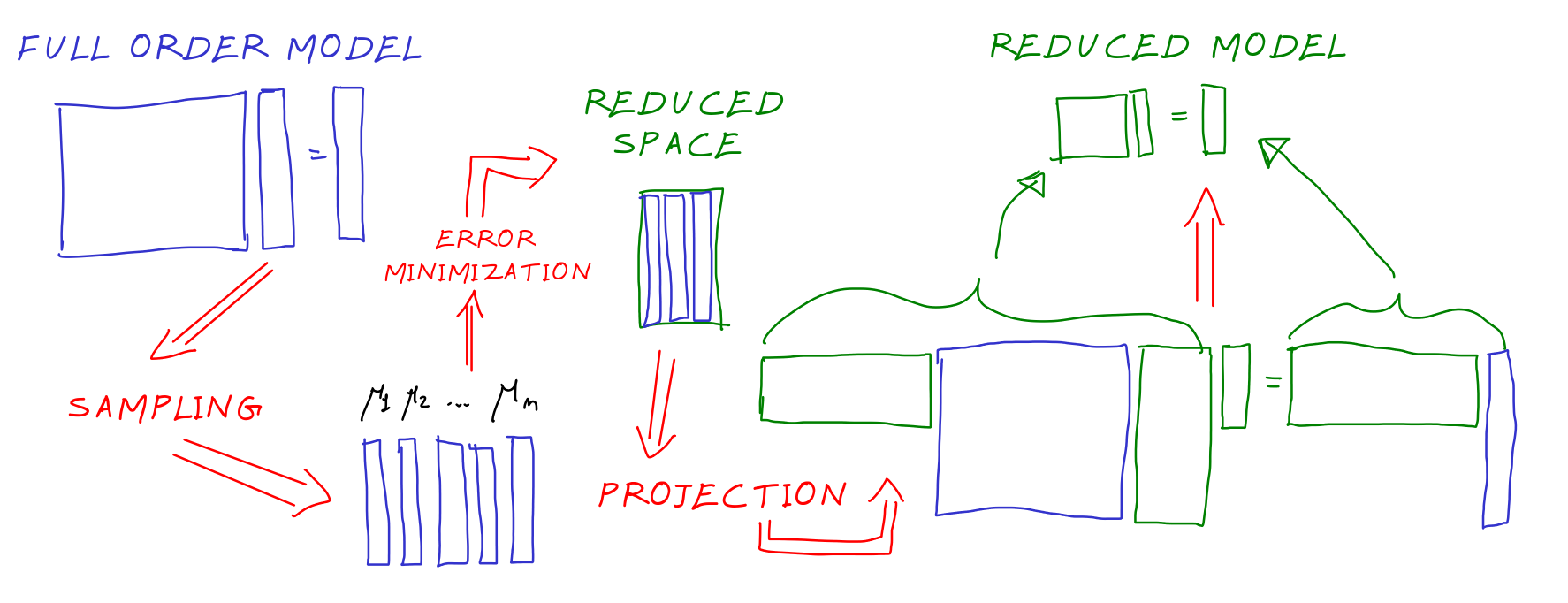
The two steps where the probability on the parameters play a role in this process are  1) The choice of the samples in the parameter domain 2) The definition of the error that we minimise to choose the reduced space.

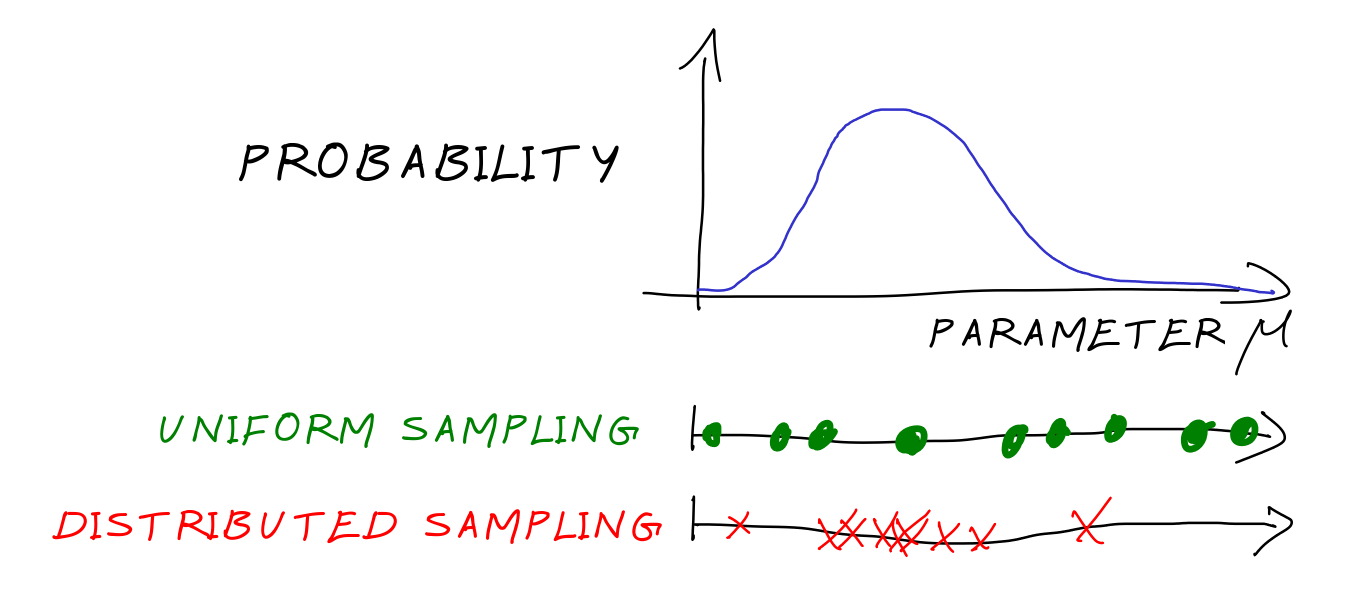
The sampling strategy is classically done with some uniform grid, some quadrature rules or randomly choosing the samples on the domain in a uniform way. The weighted algorithms adapt the sampling strategy to the probability distribution, obtaining a distributed sampling. Suppose that we know a priori that a certain situation is much more probable than another one, the algorithm will pick many more samples in the probable one. This helps in getting better results on average test cases.

The definition of the error that one tries to minimiwe while searching for the reduced space can be modified according to the underlying probability distribution. For example, one can weight such error with the probability density function. This means, again, that when we see an error in a very likely-to-happen simulation, we worry a lot and we try to improve the approximation on such parameters, while if it happens on rare events, we may ignore this piece of information.

Greedy Algorithm	POD algorithm

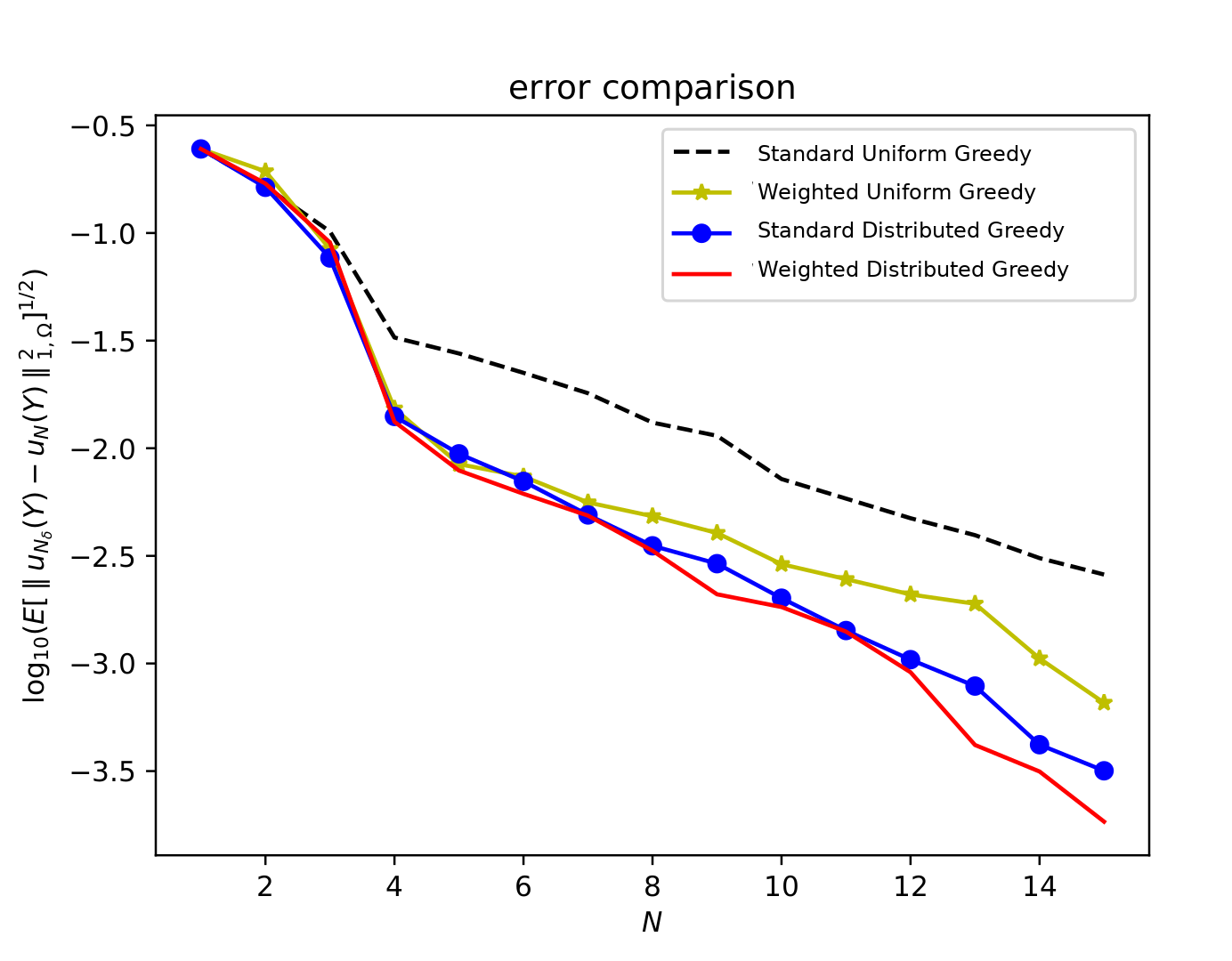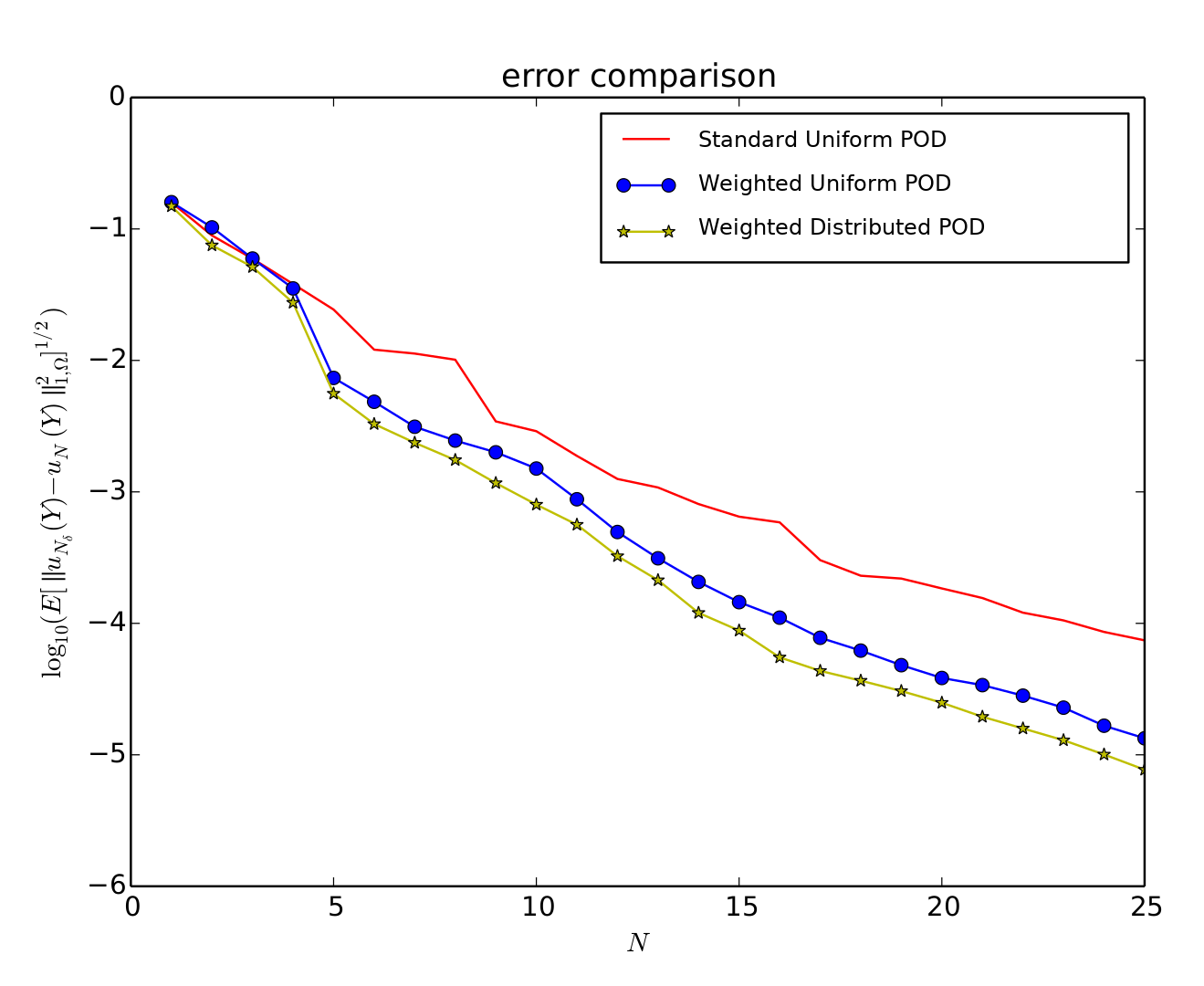Applying these two modifications to the MOR algorithms one can obtain smaller models for the same error. We have tested the Greedy algorithm and the proper orthogonal decomposition (POD) obtaining a good level of improvement. In the previous figures, one can see that the two modifications, or even one of the two, helps in getting smaller error on tests, with respect to the standard strategy. This is due to the exploitation of useful stochastic information that governs the problem inside the reduced algorithm.

This allow to get nice simulations in even shorter computational times with respect to the classical MOR algorithms. In the next figure, we can see a simulation of a convection - diffusion problem run with a weighted MOR technique.

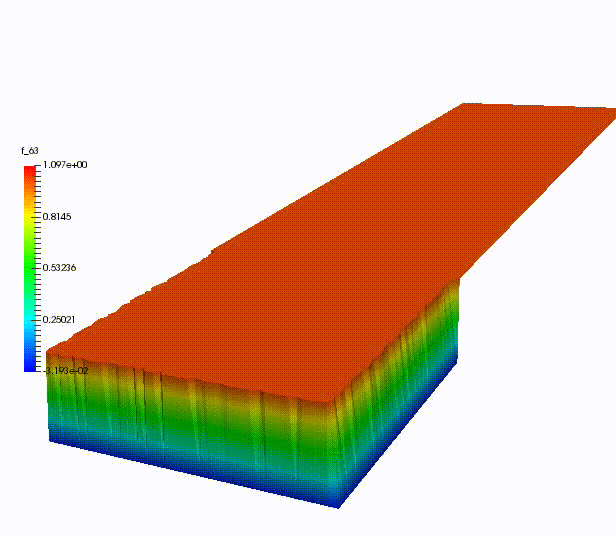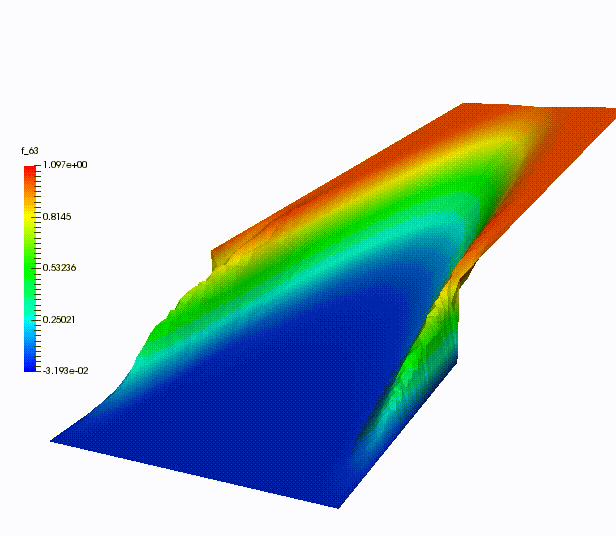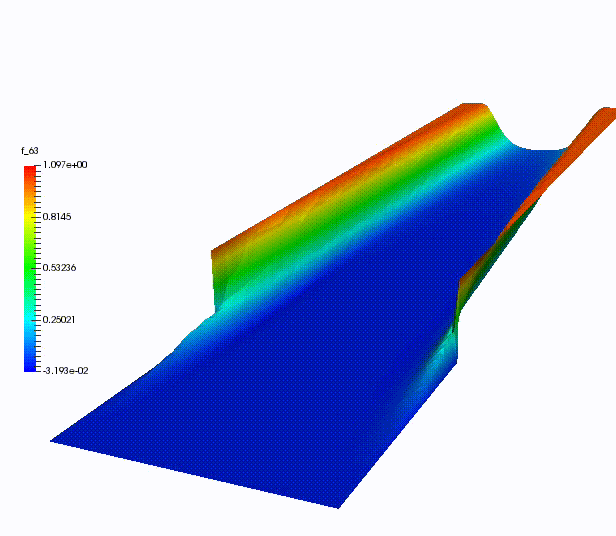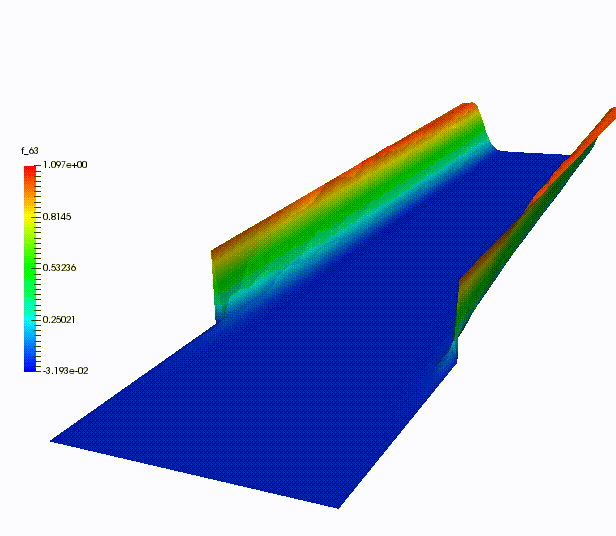
Conclusion: use all the data you have!

It is clear that in uncertain situations, the distribution of the uncertainty can provide very useful information. MOR algorithms can be designed for this and they will improve significantly in time and accuracy if this knowledge is exploited.

References

[1] D. Torlo, F. Ballarin, and G. Rozza. Stabilized Weighted Reduced Basis Methods for Parametrized Advection Dominated Problems with Random Inputs In SIAM/ASA Journal on Uncertainty Quantification 2018.

[2] L. Venturi, F. Ballarin, and G. Rozza. A Weighted POD Method for Elliptic PDEs with Random Inputs In Journal of Scientific Computing 2019.

[3] P. Chen, A. Quarteroni, and G. Rozza. A weighted reduced basis method for elliptic partial differential equations with random input data In SIAM Journal on Numerical Analysis 2013.

[4] L. Venturi, D. Torlo, F. Ballarin, and G. Rozza. Weighted Reduced Order Methods for Parametrized Partial Differential Equations with Random Inputs In: Canavero F. (eds) Uncertainty Modeling for Engineering Applications. PoliTO Springer Series. Springer, Cham.