Arbitrary High–Order Positivity–Preserving Finite–Volume Shallow–Water scheme without Restrictions on the CFL
Date:
This is a talk is about a work in collaboration with Mirco Ciallella, Lorenzo Micalizzi and Philipp Öffner.
Shallow water equation describe the evolution of the water level on a certain topography when the wave lenghts are larger than the water height. Simulating this evolution could be challenging and there are some important properties that should be maintained. First of all the water height should stay positive, not only for physical reasons, but also for numerical stability. Then, there exist some equilibrium states which are not trivially conserved by numerical schemes.
In this work, we develop and present an arbitrary high order well-balanced finite volume WENO method combined with the modified Patankar Deferred Correction (mPDeC) time integration method for the shallow water equations. Due to the positivity-preserving property of mPDeC, the resulting scheme is unconditionally positivity preserving for the water height.
The tricky part is to apply the mPDeC to the spatial semi-discretization of the shallow water equations. mPDeC can be applied onto production-destruction systems. Hence, the semidiscretized WENO5 must be rewritten into a production-destruction system, by considering the positive and negative parts of the fluxes. These are small modification inside a classical WENO5 code, as you can check out in our Git repository. This leads to a linearly implicit method, which can be easily solved with Jacobi iterative method (with few iterations). The result is a scheme that does not need any restriction on the timestep to guarantee the positivity of water height, it is very accurate (arbitrarily high order) and fast to run.
Below an example with a WENO5 mPDeC5 scheme.

Another small correction that can be applied in order to preserve equilibrium states, is to subtruct the residual of a priori known steady state solutions. This allow to much better see perturbations of these states even with coarse meshes as below.
| Not well-balanced | Well-balanced |
|---|---|
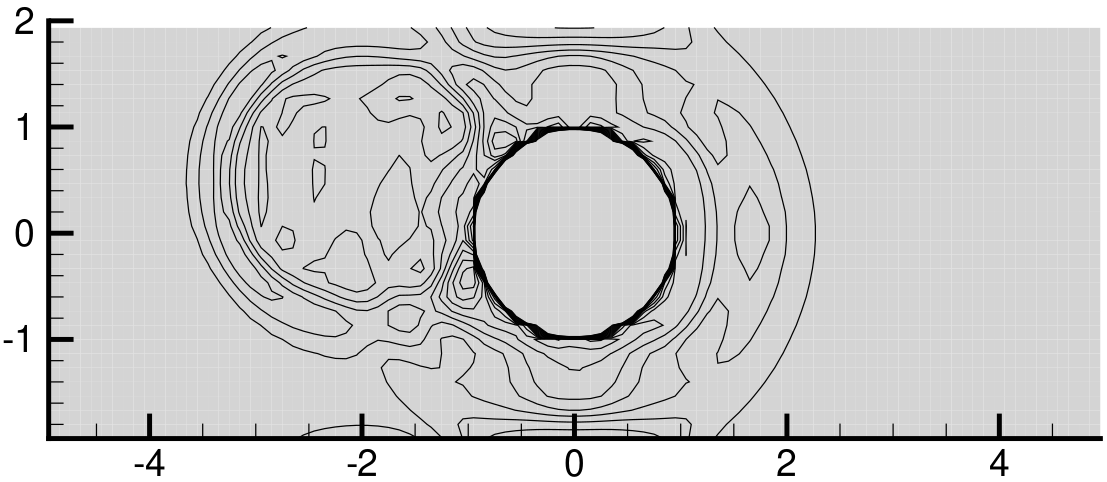 | 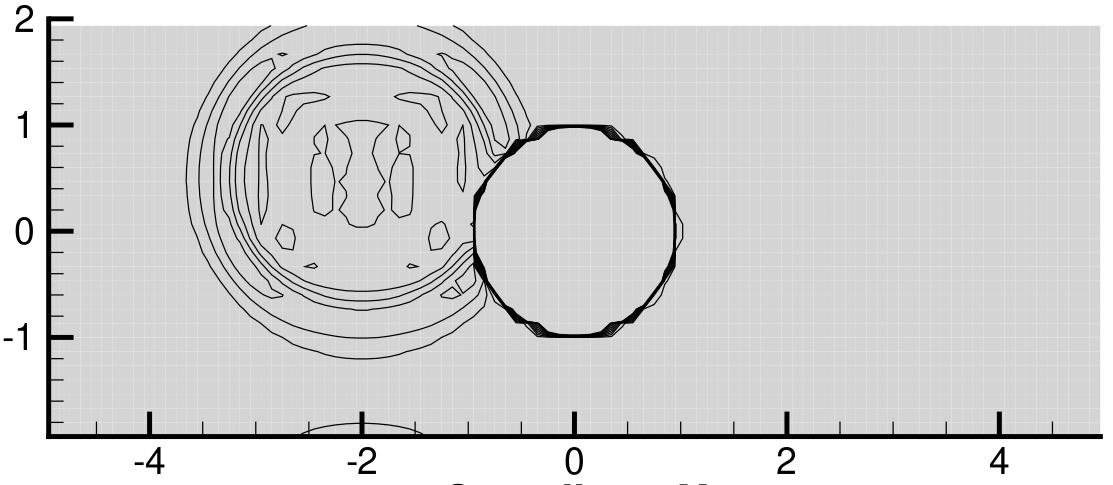 |
If you want to learn more, you find here the references and the code.
