Model order reduction for Friedrichs’ systems: a bridge between elliptic and hyperbolic problems

Friedrichs’ systems (FS) K. O. Friedrichs. Comm. Pure & App. Math, 1958 are symmetric positive linear systems of first order PDEs that can describe many well known hyperbolic and elliptic problems in a unified framework. This allows, for example, to pass from one regime to another in different areas of the domain. One of the key ingredients of FS is the possibility of rewriting higher order derivative terms of PDEs through additional variables in the system of equations with only first order terms. This leads to a formulation composed by a linear combination of many block-structured fields $\mathcal{A}^k$ applied to the unknown $z$ and its first order derivatives, i.e., \(\begin{cases} Az=f,\\ (\mathcal{D}-\mathcal{M}) z= 0, \end{cases} \qquad \text{ with } \qquad \begin{cases} Az = A_{(0)}z + A_{(1)}z,\\ A_{(0)}z = \mathcal{A}^0 z,\\ A_{(1)}z = \sum_{k=1}^d \mathcal{A}^k \partial_{x_k} z, \end{cases}\) where $\mathcal{D}$ and $\mathcal{M}$ are boundary fields, one given by the problem and the second used to impose the boundary conditions. Under some coercivity assumptions on the fields, the existence, uniqueness and well-posedness of the problem can be proven in different forms (strong, weak, ultraweak).

A series of (linear) discontinuous Galerkin (DG) methods has been proposed P. Lesaint. Numerische Mathematik, 1973 and A. Ern and J.-L. Guermond. SIAM journal on numerical analysis, (2006) to solve FS accurately. Moreover, the error analysis performed in Di Pietro and Ern. Mathematical aspects of discontinuous Galerkin methods, volume 69. Springer Science & Business Media, (2011) provides an error estimator for the methods.

Now, if one introduces physical parameters in the blocks of the fields defining the system, one obtains very different problems. In order to speed up the computational costs of many-query simulations of FS, one can resort to classical reduced order methods such as POD and greedy algorithms.

The error analysis available at the DG level can be used for a sharp error estimator in the reduced order method that certifies the accuracy of the reduced method. Moreover, it leads to an efficient offline phase for the greedy algorithm.

We will show some simulations of various problems passing through different regimes using the same framework for all of them: advection-diffusion-reaction problems, linear elasticity problems, curl-curl problems. The preliminary results show an incredible reduction in computational costs for simulating FS thanks to the reduced order method.

Linear Elasticity FOM	Linear Elasticity ROM

Curl-curl FOM	Curl-curl ROM

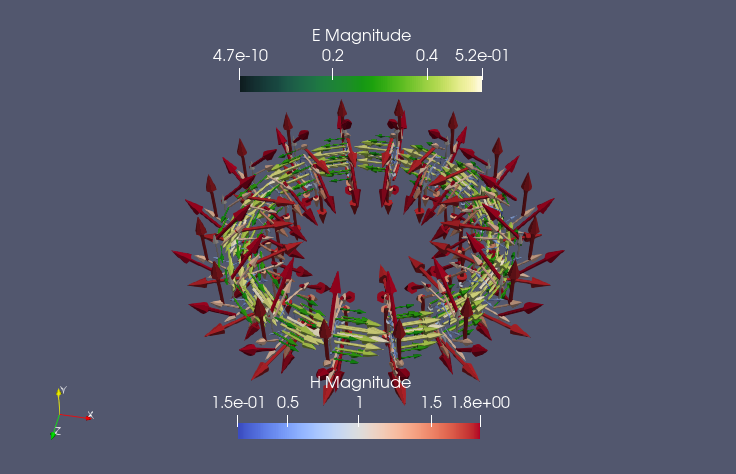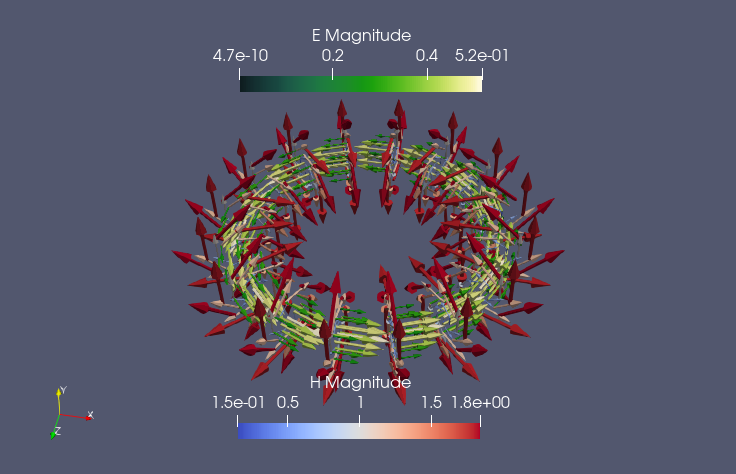Slides