A new efficient explicit Deferred Correction framework: analysis and applications to hyperbolic PDEs and adaptivity
Date:
The Deferred Correction is an iterative procedure used to design numerical methods for systems of ODEs, characterized by an increasing accuracy at each iteration. The main advantage of this framework is the automatic way of getting arbitrarily high order methods, which can be put in Runge-Kutta form, based on the definition of subtimenodes in each timestep. The drawback is a larger computational cost with respect to the most used Runge-Kutta methods. To reduce such cost, in an explicit setting, we propose an efficient modification: we remove the unnecessary subtimenodes in all the iterations, introducing interpolation processes between them. We provide the Butcher tableaux of the novel methods and we study their stability, showing that in some cases the computational advantage does not affect the stability. The flexibility of the novel modification allows nontrivial applications to PDEs and construction of adaptive methods. The good performances of the introduced methods are broadly tested on several benchmarks both in the ODE and PDE settings.
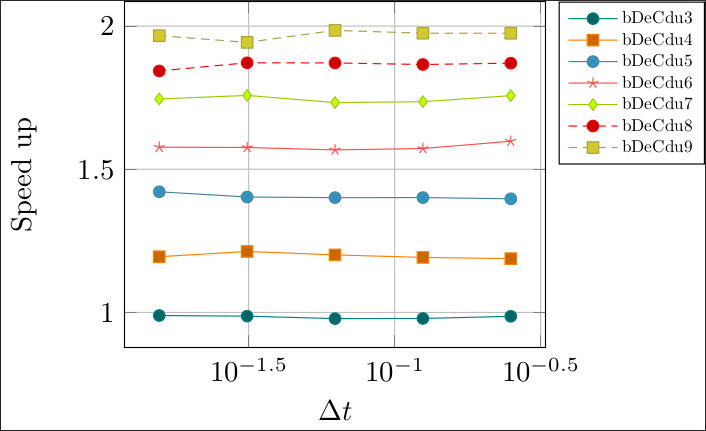
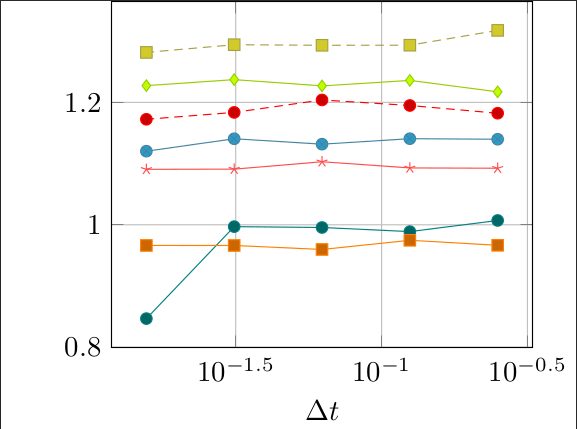
The speed up factor for a vibrating system problem
| Equispaced nodes | Gauss-Lobatto nodes |
|---|---|
 |  |
